12 Tries

Coding

Java

Algorithm

Tries

This lecture introduces the Trie data structure and its applications

Author

Jiuru Lyu

Published

May 20, 2024

Introduction

Definition 1

A String is a sequence of characters.
- Examples:
  - Digitized image
An alphabet \(\mathbf{\Sigma}\) is the set of possible characters for a family of strings:
- Examples:
  - {A, T, C, G}
We denote the alphabet size by \(|\mathbf{\Sigma}|\).

Definition 2 Let \(P\) be a string of size \(m\).

A substring \(P[i\dots j]\) of \(P\) is the subsequence of \(P\) consisting of the characters with indices between \(i\) and \(j\).
Example: “tire” is a substring of “retrieval” (with indices between \(2\) and \(5\)).

Pattern Matching Problem

Pattern Matching Problem: Given strings \(\mathbf{T}\) (text) and \(\mathbf{P}\) (query), the pattern matching problem consists of finding a substring of \(\mathbf{T}\) equal to \(\mathbf{P}\).

Applications:
- Text editors
- Search engines
- Bioinformatics

Pattern Matching: Brute-Force Method
- The Brute-Force pattern matching algorithm compares the key \(\mathbf{P}\) with the text \(\mathbf{T}\) for each possible shift of \(\mathbf{P}\) relative to \(\mathbf{T}\) until either
  - a match is found, or
  - all placements of the pattern have been tried.

/**
 * This method finds the first occurrence of the query in the text.
 * @param text the text to search
 * @param query the query to search for
 * @return the index of the first occurrence of the query in the text, or -1 if the query is not found
 */
public static int findBrute(char[] text, char[] query) {
    int n = text.length;
    int m = query.length;
    for (int i = 0; i <= n - m; i++) { // test shift i of the pattern
        int k = 0;
        while ( k < m && text[i + k] == query[k] )
            k++;
        if (k == m) return i; // match at i
    }
    return -1; // no match found
}

The time complexity of the Brute-Force pattern matching algorithm is \(\mathcal{O}(nm)\).
- In real world, \(n\) is usually very large, so this algorithm is not efficient.

Trie Data Structure

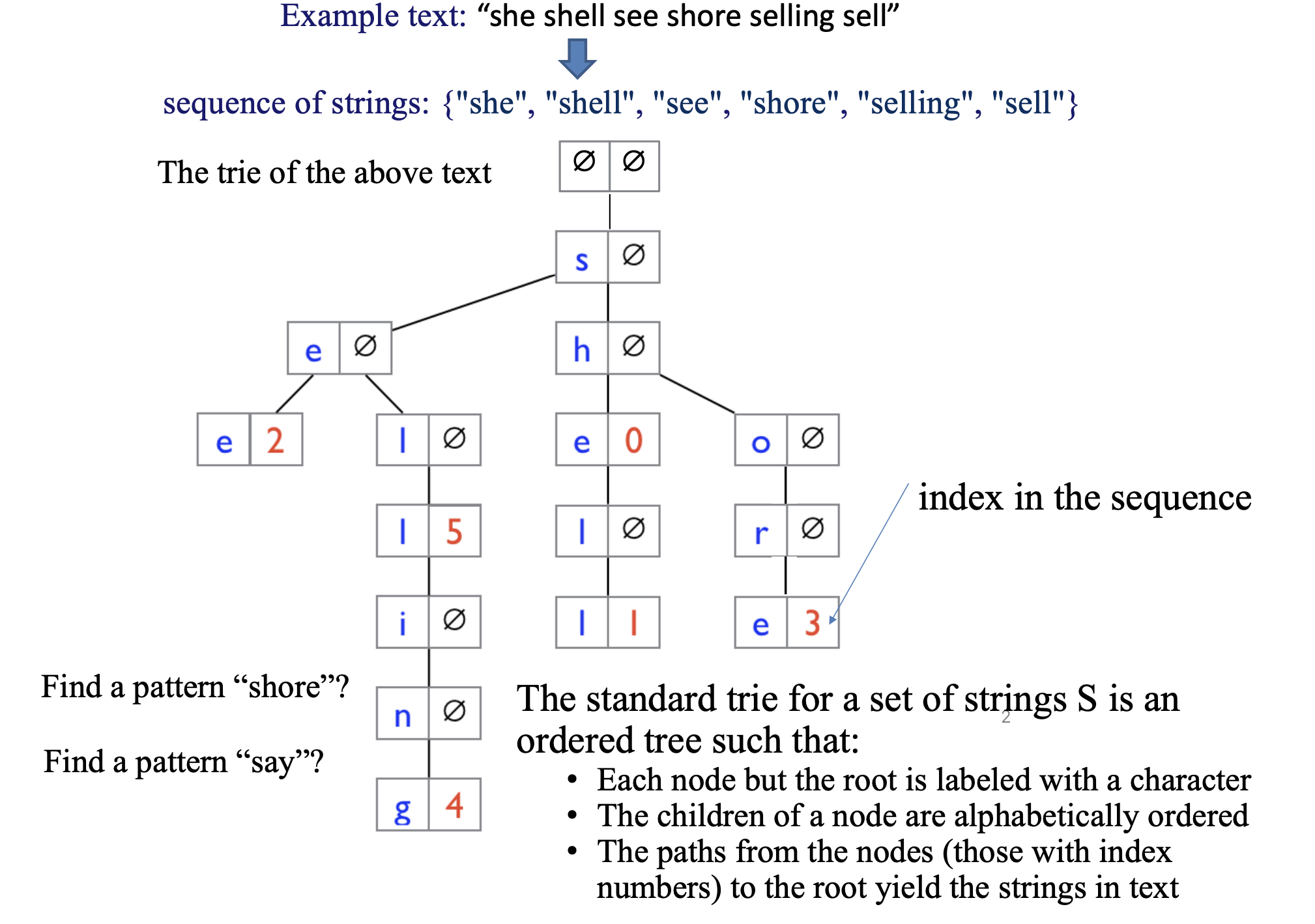
The standard trie for a set of strings \(S\) is an ordered tree such that:
- Each node but the root is labeled with a character
- The children of a node are alphabetically ordered
- The paths from the nodes (those with index numbers) to the root yield the strings in text.

Improvement on Trie: Compressed Trie

Definition 3 Let \(P\) be a string of size \(m\).

A substring \(P[i\dots j]\) of \(P\) is the subsequence of \(P\) consisting of the characters with indices between \(i\) and \(j\).
- Example: “tire” is a substring of “retrieval” (with indices between \(2\) and \(5\)).
A prefix of \(P\) is a substring of the type \(P[0\dots i]\)
- Example: “ret” is a prefix of “retrieval” (with indices between \(0\) and \(2\)).
A suffix of \(P\) is a substring of the type \(P[i\dots m-1]\)
- Example: “eval” is a suffix of “retrieval” (with indices between \(5\) and \(8\)).

Compressed Tries
- Problem: the space complexity of a trie is \(\mathcal{O}(n|\mathbf\Sigma|)\), where \(n\) is the number of strings in the trie. This is not efficient when \(n\) is large.
- We can compress the trie by Compressing each chain of single-child nodes into a node.
  - In this case, each internal node has at least two children.
- Claim: The space complexity of a compressed trie is \(\mathcal{O}(s|\mathbf{\Sigma}|)\), where \(s\) is the number of strings.
Proof.
The number of leaves is equal to the number of strings \(s\). Moreover, the number of internal nodes is no more than the number of leaves \(s\) because each internal node has multiple children. Therefore, the number of node is no more than \(2s\). Since each node has \(\mathcal{O}(|\mathbf{\Sigma}|)\) space, the total space complexity should be \(\mathcal{O}(2s|\mathbf{\Sigma}|)\sim\mathcal{O}(s\cdot|\mathbf{\Sigma}|).\qquad\blacksquare\)

Search for Substring

The trie we built until now can only allow us to match the whole word or match the prefix.

Suppose we want to search if a given key is a substring of the string “minimize.”

The Brute-Force algorithm will have \(\mathcal{O}(mn)\) time complexity.
To speed up, we can enumerate all the suffixes of “minimize”: “e”, “ze”, “ize”, “mize”, “imize”, “nimize”, “inimize”, “minimize”.
Then, we can organize them into a trie, and enjoy \(\mathcal{O}(m)\) time complexity to search for the query.
If we can find the query to be a prefix of any suffix, then the query is a substring of the string.

Though the time complexity is \(\mathcal{O}(m)\), the space complexity is \(\mathcal{O}(m^2)\), which is not efficient.
Suffix trie: compact representation.
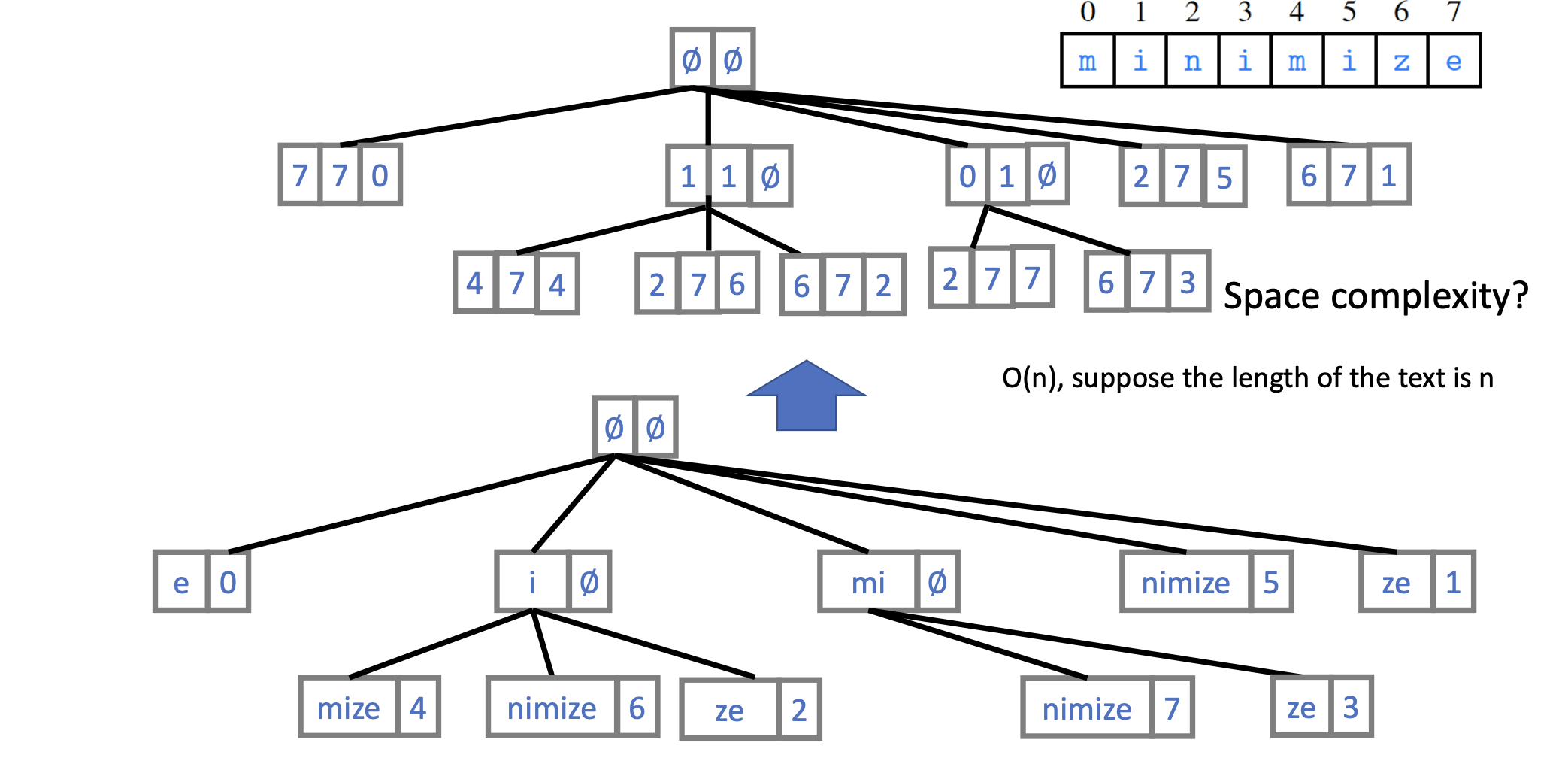
- This way we enjoy linear space complexity as well.

Application of Tries: Data Compression by Huffman Coding

Compression reduces the size of a file:
- To save space when storing it
- To save time when transmitting it
- Most files have lost of redundancy
Who needs compression?
- Moore’s Law: number transistors on a chip doubles every 18 months
- Parkinson’s Law: data expands to fill the space available for storage
- Text, images, sound, video, etc.
Applications:
- Generic file compression:
  - Files: GZIP,BZIP,7z.
  - Archivers: PKZIP.
  - File systems: NTFS, HFS+, ZFS.
- Multimedia.
  - Images: GIF,JPEG.
  - Sound: MP3.
  - Video: MPEG, DivXTM, HDTV.
- Communication.
  - ITU-T T4 Group 3 Fax.
  - V.42bis modem.
  - Skype.
- Databases. Google, Facebook, ….
String data with space efficiency:
- All of the types of data we process with modern computer systems have something in common: They are ultimately represented in binary
- If we can represent the data in fewer bits, we can save space.
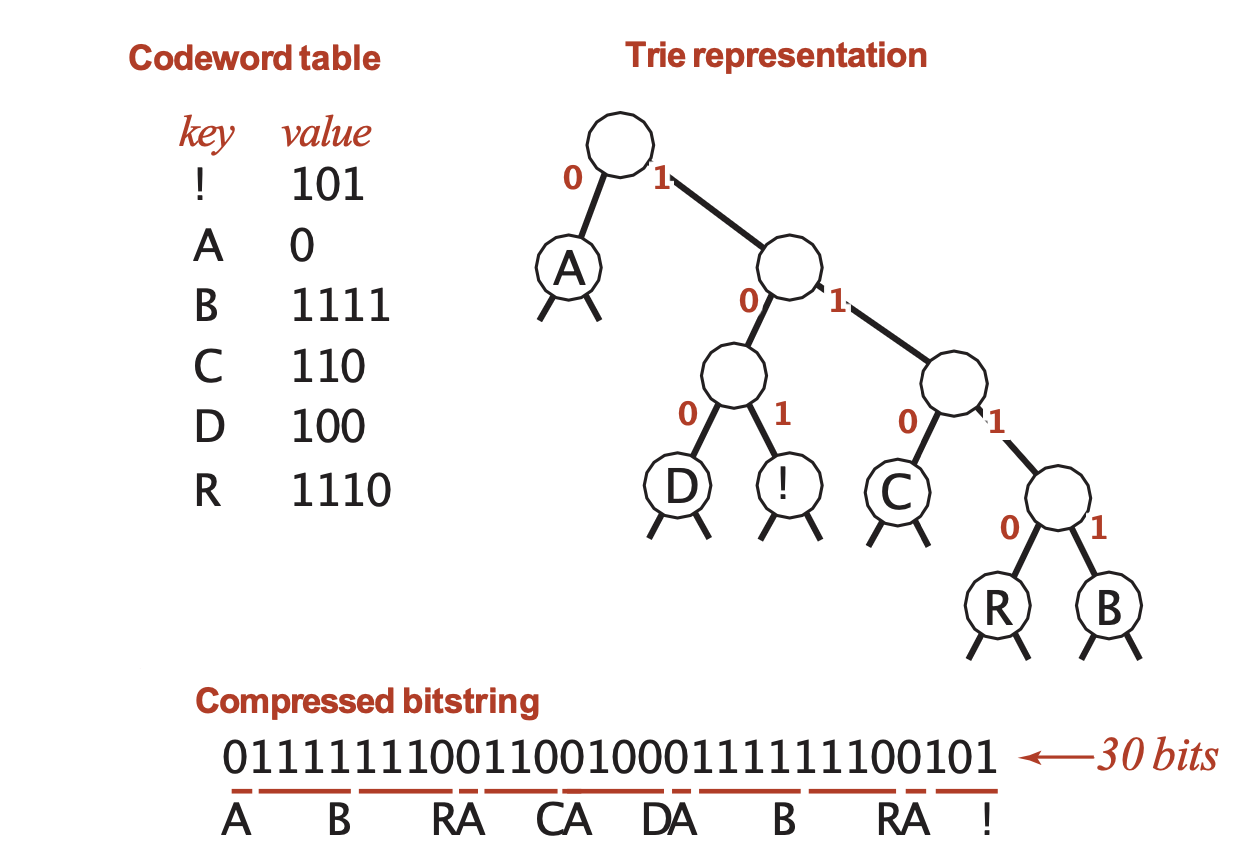
- However, if we simply use, say, A:0, B:1, R:00, C:01, D:10, I:11, we will have ambiguity.
  - This is because some of the codes are prefixes of others.
  - For example, the code for “A” is a prefix of the code for “R”.
- We need a code that is prefix-free.
  - This means that no code is a prefix of any other code.
  - This is also called a prefix code.
Prefix-free codes: compression and expansion
- A binary trie representation
  - Ordered children: 0 leads to left child, 1 leads to right child.
  - Each leaf holds a character
Huffman Enconding Trie Overview
- How to obtain the best prefix-free code?
  - Frequently-used characters with shorter code
  - So, they are closer to the root
  - We will use a bottom-up constructing algorithm to build a trie from least frequent to most frequent characters.
    - Step 1: Get all the characters’ frequencies for string
      - We build \(|\mathbf{\Sigma}|\) singleton tries, namely trie with only one node.
    - Step 2: Bottom-up construction from least frequent nodes
      - In each iteration, we pick up two lowest frequency tries and merge them into a single trie whose frequency is the sum of these two tries.
      - We iterate until all merged into a single trie.

Proposition 1 (Proposition) Huffman algorithm produces an optimal (no prefix-free code uses fewer bits) prefix-free code for a given set of character frequencies.

Time complexity of Huffman algorithm:
- \(\mathcal{O}(|\mathbf{\Sigma}|\cdot\log|\mathbf{\Sigma}|)\), where \(|\mathbf{\Sigma}|\) is the alphabet size (R in the code implementation).
Using Huffman encoding for data compression:
- Dynamic model: Use a custom prefix-free code for each message.
- Compressing:
  - Read message
  - Built prefix-free code for message
  - Compress message using prefix-free code
- Uncompressing:
  - Read compressed message and expand it using prefix-free code
Applications of Huffman encoding:
- JPEG, MP3, MPEG, ZIP, etc.
- Google, Facebook, etc.
- Communication systems: Skype, etc.